Competitive Research Grants
Research Project FONDECYT Regular Nº 1210915
(2021 -2024)
“Systematic tail risk: new directions for understanding high-dimensional extreme financial risk”.
Our main research questions concern how high-frequency (intraday) returns improve our understanding of extreme events’ dynamic properties and how realized measures of extreme events could be valuable predictors of the occurrence, magnitude, and tail dependence of future extreme events. Further, how high-frequency data facilitate the modeling and forecasting of systemic tail risk and how extreme events of high-frequency trading are related to the strength of spatial dependence and financial stability. This research project will pursue three main objectives: i) to develop an econometric framework for systemic tail risk modeling where the dynamic of extreme events in financial markets at high frequency will play an important role, ii) to propose a novel multivariate framework with realized measures based on information obtained from intraday high-frequency extreme events, iii) to study the relationship between extremes and financial spatial dependence in financial markets.

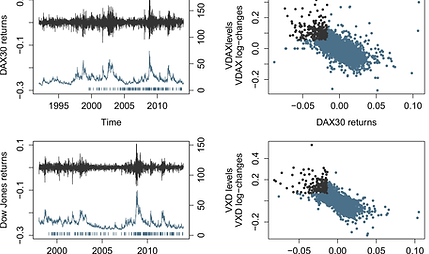
Research Project FONDECYT Regular Nº 1180672
(2018 -2020)
“Modeling high-dimensional and high-frequency extreme events in financial markets: Incorporating trading activity, liquidity measures, and news flow”.
In risk management, extreme losses of a stock market or the conditional losses of multiple risk factors are of great concern to all investors. What determines susceptibility to extreme losses in financial markets and the cluster behavior of these events? How many transactions or how long does it take for new information to be reflected in prices and possible extreme losses? In which markets is this information revealed faster? Do times of greater activity coincide with a higher number of extreme events present in the market? Do we observe a weaker clustering behavior of extreme events for firms and stock markets with better transparency in its public information? Did high-frequency trading in the last decade increase the intensity of this class of events in different financial markets, and therefore, the global systemic risk?
Research Project FONDECYT Regular Nº 1150349
(2015 -2017)
“Extreme Financial Risk: A Multivariate Conditional Framework of Extreme Events”.
The recent global crises during the last years has one more time demonstrated the importance of investigate the dynamic behaviour of extreme events during period of crises. In a world of complex financial instruments with the dramatic increase in available information and historical market data, it makes necessary the development of new methodologies to describe the dynamics of these events.
Extreme value theory (EVT) is considered to provide the basis for the statistical modelling of such extremes. The potential of extreme value theory applied to financial problems and in particular within the quantitative risk framework are unlimited. EVT has showed its major influence in extreme risk modelling with measures that attempt to describe the size and probability of occurrence of such losses. Indeed, results of EVT have been applied on different areas of risk management as for example, portfolio credit risk, operational risk, high-frequency trading and jump-diffusion models.
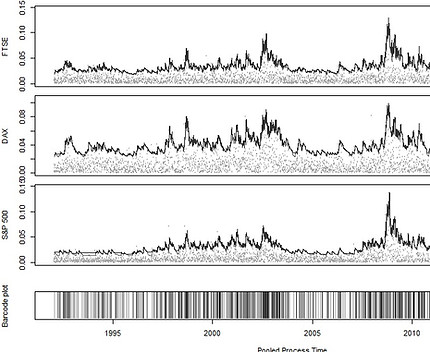

Research Project FONDECYT Initiation Nº 11110247
(2011 -2013)
“Advanced extremal models for Risk Modeling under Basel II”.
Many fields of modern science and engineering have to deal with events which are rare but have significant consequences. Extreme value theory is considered to provide the basis for the statistical modelling of such extremes. The potential of extreme value theory applied to financial problems and in particular within the Basel II framework has only been recognized recently. This project aims at introducing a new methodology in extreme value theory as well as practical aspects for estimating and assessing statistical models for risk measures. In particular, this project looks at ways of extending the classical extreme value models to obtain a joint description of both the severity and dynamical frequency of losses exceeding high thresholds. We use the marked point process approach to extreme values to obtain the joint description